Koch snowflake หรือเกล็ดหิมะค็อค เป็นเส้นโค้งแบบแฟร็กทัล (Fractal curve) ซึ่งล้อมรอบพื้นที่ที่จำกัด แต่มีเส้นรอบวงเป็นอนันต์ ซึ่งถือได้ว่าเป็นความสุดยอดของสิ่งนี้เลย
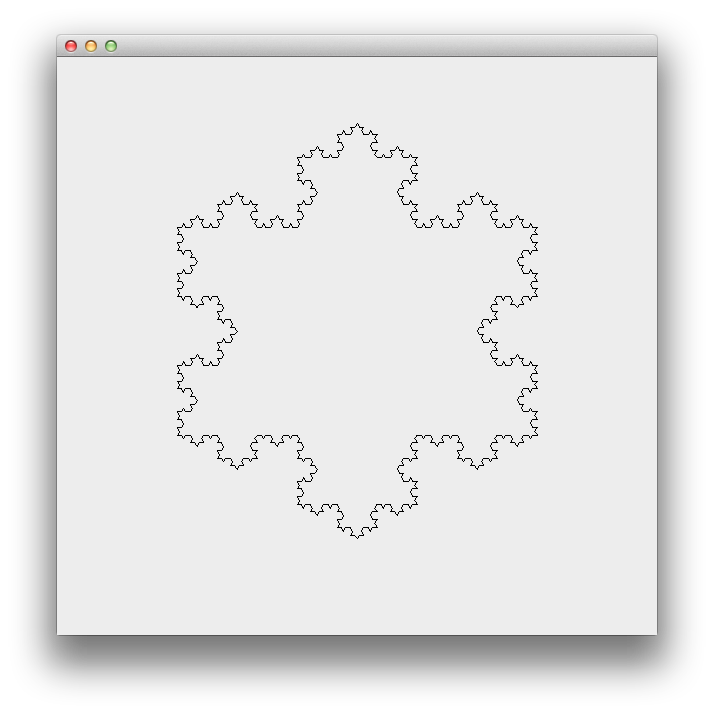
ถ้าใครนึกภาพไม่ออกลองมาดูภาพเกล็ดหิมะค็อคที่สร้างจากรูปสามเหลี่ยมด้านเท่าโดยทำซ้ำ 7 รอบแรกกันครับ

มาถึงตอนนี้หลายคนอาจเริ่มสงสัยแล้วว่า เอ๊ะ แล้วความรู้ทางคณิตศาสตร์เรื่องนี้ มันมีประโยชน์อะไรนอกจากเอามาวาดรูปเกล็ดหิมะล่ะ?
เราพบความมหัศจรรย์นี้ได้ในเรื่องของ “แผนที่” เช่น ระหว่างไทย-กัมพูชา เราเถียงกันเรื่องใช้แผนที่ 1:200000 หรืออะไรก็ดี คำถามคือความยาวเขตแดนระหว่างไทย-กัมพูชามีเท่าไรกันแน่ หรือคำถามที่ว่า ถ้าเราซื้อที่ดินริมหาด ที่ดินริมหาด ส่วนใหญ่ราคาจะขึ้นอยู่กับว่ามีหาดยาวเท่าใด (ติดหาดกี่เมตรนั้นเอง) หรือ คำถามว่า เกาะอังกฤษมีความยาวรอบรูปเท่าใด เช่นถ้าเรามีเทคโนโลยีที่ที่สามารถวัดแบบไม่ละเอียดเราอาจจะได้ค่าค่าหนึ่ง แต่ถ้าเรามีเทคโนโลยีที่วัดได้ละเอียดขึ้นไปอีกก็เหมือนกับว่า เราจะมีความยาวรอบเกาะที่เพิ่มขึ้น และถ้าเราวัดได้ไปถึงระดับมิลลิเมตร ไม่ยิ่งยาวไปกันใหญ่เหรอ และถ้าวัดไปถึงระดับอะตอมล่ะ!
ว้าว! ฟังดูน่าสนใจขึ้นมาหรือยังครับ ใครสนใจอยากอ่านเพิ่มเติมก็ไปอ่านได้ที่ https://en.wikipedia.org/wiki/Koch_snowflake
หลังจากเกริ่นมาพอสมควรแล้ว คิดว่าทุกคนน่าจะอยากรู้แล้วว่า เราจะเขียนโปรแกรมเพื่อสร้างเจ้า Koch snowflake นี่ได้อย่างไร ดังนั้น วันนี้เราจะมาเขียนโปรแกรมภาษา Java เพื่อสร้าง Koch snowflake โดยใช้ความรู้เรื่อง Recursive เข้ามาช่วยกันครับ
วิธีวาดรูป Koch snowflake
1. แบ่งเส้นตรงออกเป็นสามส่วนเท่า ๆ กัน
2. วาดสามเหลี่ยมด้านเท่าให้มีฐานเป็นส่วนกลางของขั้นตอน 1 และมียอดชี้ออกด้านนอก
3. ลบเส้นส่วนที่เป็นฐานของสามเหลี่ยมในขั้นตอน 2 ออก
ทำซ้ำขั้นตอนที่ 1-3 ไปเรื่อย ๆ จนกว่าจะได้รูปเกล็ดหิมะที่ถูกใจ
เขียน Code กันเลย
import java.awt.Graphics;
import java.awt.Graphics2D;
import javax.swing.JFrame;
public class KochSnowFlake extends JFrame
{
private static final long serialVersionUID = 1L;
int num=1;
public KochSnowFlake()
{
setSize(600, 600);
setDefaultCloseOperation(EXIT_ON_CLOSE);
setVisible(true);
Thread t= new Thread(new Runnable()
{
@Override
public void run()
{
while(true)
{
for(int i=1;i<= 10;i++)
{
try
{
Thread.sleep(6000 );
} catch (InterruptedException e)
{
// TODO Auto-generated catch block
e.printStackTrace();
}
num=i;
repaint();
}
}
}
});
t.start();
}
public void paint(Graphics g)
{
super.paint(g);
Graphics2D gg=(Graphics2D)g;
Vector now= new Vector(getWidth() / 5.0, getHeight()/3.0*2.0);
Vector dir_with_size= new Vector(getWidth() /5.0*3.0, 0);
dir_with_size= dir_with_size.rotate(Math.PI/3);
createSnowFlake( gg , now, dir_with_size, num);
now= now.add(dir_with_size);
dir_with_size= dir_with_size.rotate(-Math.PI/3*2);
createSnowFlake( gg , now, dir_with_size, num);
now= now.add(dir_with_size);
dir_with_size= dir_with_size.rotate(-Math.PI/3*2);
createSnowFlake( gg , now, dir_with_size, num);
}
public void createSnowFlake(Graphics2D g , Vector now,Vector dir_with_size,int n)
{
if(n==0) return;
if(n==1)
{
Vector a,d;
a = now;
d = dir_with_size.add(now);
g.drawLine((int)a.x,(int)a.y, (int)d.x,(int)d.y);
return;
}
Vector a,b,c,d;
a = now;
b = dir_with_size.mul(1.0/3.0).add(now);
c = dir_with_size.mul(2.0/3.0).add(now);
d = dir_with_size.mul(1).add(now);
Vector dir_with_size2= dir_with_size.rotate(Math.PI /3.0).mul(1.0/3.0);
Vector start3 = dir_with_size2.add(b);
Vector dir_with_size3= c.sub(start3) ;
createSnowFlake( g , b, dir_with_size2, n-1);
createSnowFlake( g , start3, dir_with_size3, n-1);
createSnowFlake( g , a, dir_with_size.mul(1.0/3.0), n-1);
createSnowFlake( g , c, dir_with_size.mul(1.0/3.0), n-1);
}
public static void main(String[] args)
{
new KochSnowFlake();
}
}
class Vector
{
public double x,y;
public Vector(){}
public Vector (double xx,double yy)
{
x=xx;
y=yy;
}
public Vector rotate(double angle)
{
double xx,yy;
double c = Math.cos(angle);
double s = Math.sin(angle);
xx = x*c + y*s;
yy = -x*s + y*c;
return new Vector(xx,yy);
}
public Vector mul(double m)
{
return new Vector(x*m,y*m);
}
public Vector add(Vector v)
{
return new Vector(x+v.x,y+v.y);
}
public Vector sub(Vector v)
{
return new Vector(x-v.x,y-v.y);
}
}
เสร็จแล้วครับ Code สั้น ๆ ไม่ยากเกินไปใช่ไหมครับ ถ้าใครงงก็ไม่ต้องตกใจหรือเสียกำลังใจไป เดี๋ยวเรียนคอร์ส Java หรือคอร์สหลักภาษาอื่น ๆ ของ EPT จบเรื่อง Recursive กับ OOP ก็จะเข้าใจ Code นี้ได้อย่างง่าย ๆ เลยครับ
แล้วลองเอาไปวาดรูปเล่นกันดูนะครับ :)
Tag ที่น่าสนใจ: koch_snowflake fractal_curve recursive_programming java_programming programming_tutorial mathematics geometric_shapes programming_languages computer_science algorithm creative_coding
หากมีข้อผิดพลาด/ต้องการพูดคุยเพิ่มเติมเกี่ยวกับบทความนี้ กรุณาแจ้งที่ http://m.me/Expert.Programming.Tutor
085-350-7540 (DTAC)
084-88-00-255 (AIS)
026-111-618
หรือทาง EMAIL: NTPRINTF@GMAIL.COM

Copyright (c) 2013 expert-programming-tutor.com. All rights reserved. | 085-350-7540 | 084-88-00-255 | ntprintf@gmail.com
