กราฟเป็นการเก็บข้อมูลในอีกรูปแบบหนึ่งที่เก็บข้อมูลไว้และมีการเชื่อมต่อกับข้อมูลถัดๆไปคล้ายกับต้นไม้คือมีลักษณะไม่เชิงเส้น (non-linear list) แต่กราฟก็ต่างจากต้นไม้เช่นเดียวกันเพราะในขณะที่กราฟมีลักษณะพ่อมีลูกได้หลายตัวแต่ลูกมีพ่อมีพ่อได้แค่หนึ่งเดียว ในขณะที่กราฟนั้นไม่มีข้อจำกัดเรื่องนี้ กล่าวคือมีตัวก่อนหน้าและตัวถัดไปอย่างไรก็ได้

กราฟ

            โหนดที่ใช้เก็บข้อมูลในกราฟเรียกว่า เวอร์เท็กซ์(vertex/ (pl.) vertices) และในแต่ละเวอร์เท็กซ์จะมีเส้นเชื่อมหากัน(คล้ายต้นไม้) แต่มีชื่อเรียกว่า เอดจ์(edges) กราฟจึงถือเป็นกลุ่มของ เวอร์เท็กซ์และเอดจ์

            กราฟเขียนแทนด้วยเซ็ต โดยเป็นเซ็ตของ เวอร์เท็กซ์และเอดจ์ นั่นเอง แต่ถ้ากราฟไม่มีสมาชิกเลยเรียกว่า null graph

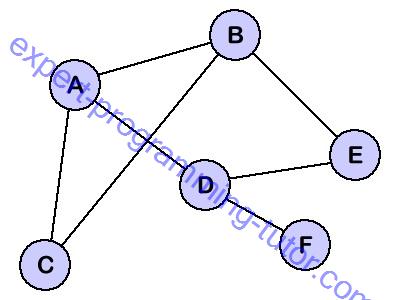รูป9-1

ให้ V แทนเซ็ตของเวอร์เท็กซ์ และ E แทนเซ็ตของเอดจ์ จะได้

V = { A, B, C , D. E, F}

E = {{A,B} , {A,C} , {A,D} , {B,E} , {B,C} , {D,E} , {D,F}}

กราฟ จะเป็นกราฟเรียบง่าย (Simple Graph) ก็ต่อเมื่อ

1.ต้องไม่มีการวนลูปของเอจด์เกิดขึ้นใน เซ็ต E หรือมี Path(A,A)

2.ต้องไม่มีเอจด์มากกว่าหนึ่งเชี่อมต่อกันระหว่างสองเวอร์เท็กซ์

ส่วนกราฟที่ไม่เรียบง่าย เรียกว่า มัลติกราฟ (Multi-graph)

กราฟมี 2 ประเภท ได้แก่

1.      Directed graph (รูป1)

หรือเรียกว่ากราฟทิศทาง เป็นกราฟแบบที่เอดจ์มีหัวลูกศรชี้ไปยังเวอร์เท็กซ์ถัดไป ซึ่งจะเรียกเอดจ์ที่มีหัวลูกศรว่าอาร์ค(arc) เช่นกรณีต้องการทำแผนที่การเดินทางจากกรุงเทพไปภูเก็ตก็ต้องใช้ทิศทางบอกจากว่าผ่านจังหวัดไหนบ้าง

2.      Undirected graph (รูป2)

ตรงข้ามกับข้างบนกราฟแบบนี้เอดจ์จะเป็นเส้นธรรมดาไม่มีเป็นหัวลูกศร หมายความว่าการเชื่อมโยงระหว่างเวอร์เท็กซ์เป็นลักษณะกลับไปมาระหว่างกันได้

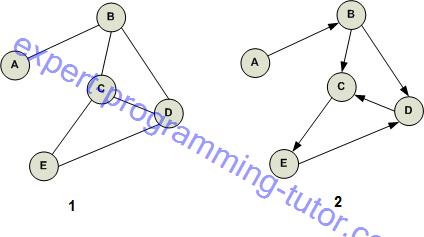รูป9-2

เรื่องของกราฟ

Path

            พาธเป็นเส้นทางระหว่างเวอร์เท็กซ์ 2 เวอร์เท็กซ์ที่อยู่ติดกัน โดยพาธนั้นมีทั้งใน Directed graph และ Undirected graph ตัวอย่างของพาธ เซ็ตของเอดจ์ในรูป 9-1 E = {{A,B} , {A,C} , {A,D} , {B,E} , {B,C} , {D,E} , {D,F}}

Cycle and Loop

            ไซเคิลเป็นกลุ่มของเวอร์เท็กซ์ที่มีจุดเริ่มกับจุดสิ้นสุดของเวอร์เท็กซ์เป็นตัวเดียวกัน เช่นรูป9-2 รูป 1 มีเวอร์เท็กซ์ B C E D B คือเริ่มจาก B แล้วกลับมาที่ B เหมือนเดิม ในขณะที่ 9-2 รูป 2 ทำไม่ได้เพราะมีทิศทางเดียว ส่วนลูปคือเอดจ์จากตัวเองไปสู่ตัวเองเท่านั้น

Adjacent vertex

               เป็นเวอร์เท็กซ์ที่อยู่ติดดินมีเอกจ์หรืออาร์คลากเชื่อมถึงกัน เช่น 9-2 รูป 1 A เป็น adjacent vertex ของ B และ B เป็น adjacent vertex ของ A แต่รูป 9-2 รูป2 B เป็น adjacent vertex ของ A แต่ A ไม่เป็น adjacent vertex ของ B

การเก็บข้อมูลของกราฟ

               การเก็บข้อมูลในกราฟมี 2 วิธีคือ การเก็บด้วยตารางและการเก็บด้วย list

Adjacency Matrix

               เป็นการเก็บข้อมูลเมทริกในการจัดเก็บเอดจ์ โดยถ้าเวอร์เท็กซ์นั้นมีเอดจ์เชื่อมโยงระหว่างเวอร์เท็กซ์ เมทริกจะมีค่าเป็น 1 แต่ถ้าไม่มีก็มีค่าเป็น 0 ถ้าเป็น undirected graph จะเขียนเลข 1 ตรงตารางทั้งคู่ของ adjacent vertex แต่ถ้าเป็น directed graph จะมีลูกศรเป้นตัวกำหนดให้ใส่เลข 1 เฉพาะเวอร์เท็กซ์ที่หัวลูกศรชี้อยู่

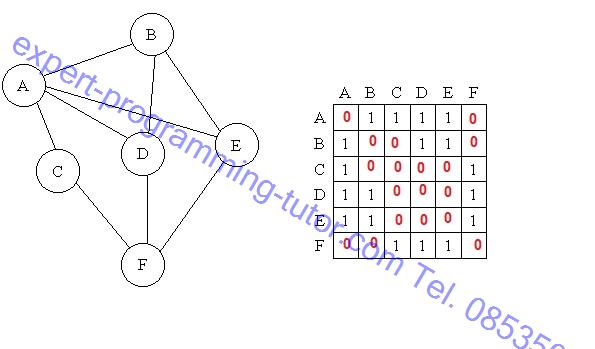รูป9-3

               ตัวอย่างของ undirected graph จาก A ไป A คือจากตัวเองไปหาตัวเองถือว่าเป็น 0 เพราะเฉพาะนั้นช่องที่ซ้ำกันระหว่างแนวตั้งและแนวนอนจึงถือเป็น 0 ทั้งหมด แถวแนวตั้งทางซ้ายคือจาก แถวแนวนอนด้านบนคือไปถึง จะเห็นได้วา B ไป C ไม่มีก็เป็น 0 แต่ B ไป E มีก็เป็น 1

               ถ้าเป็นกรณีของ directed graph จะใส่เลข 1 ที่ช่องที่หัวลูกศรชี้ไปเช่น สมมติชี้จาก A ไป B จะใส่เลข 2 ที่ช่องที่ A อยู่ทางซ้ายและ B อยู่ข้างบน แต่ช่องที่ B อยู่ทางซ้ายและ A อยู่ข้างบน นั้นใส่เลข 0

Adjacency List

               ตามชื่อก็คือการเก็บข้อมูลแบบ Adjacency List จะใช้ลิงค์ลิสต์ในการเก็บข้อมูล โดยจะใช้ singly linked list สำหรับเก็บเวอร์เท็กซ์ต่างๆ

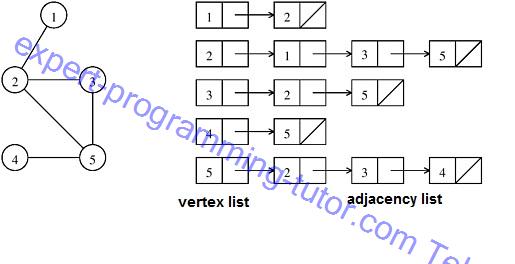รูป9-4

            ช่องแรกสุดจะเก็บลิสต์ของเวอร์เท็กซ์ ก็คือเวอร์เท็กซ์ทุกเวอร์เท็กซ์ ในขณที่ช่องที่ 2 เป็นต้นไปจะเก็บเวอร์เท็กซ์ที่ติดกับเวอร์เท็กซ์ลิสต์

Weighted graph

            เป็นกราฟแบบที่ระบุค่าไปบนเอดจ์ด้วย  เพราะในความเป็นจริงกราฟเป็นสิ่งถูกประยุกต์ใช้งานเป็นจำนวนมาก เช่นการทำแผนที่เพื่อคำนวณระยะทางก็จะใช้กราฟแล้วระบุระยะทางหว่างเวอร์เท็กซ์ซึ่งแทนจังหวัด หรือ ประเทศก็ได้

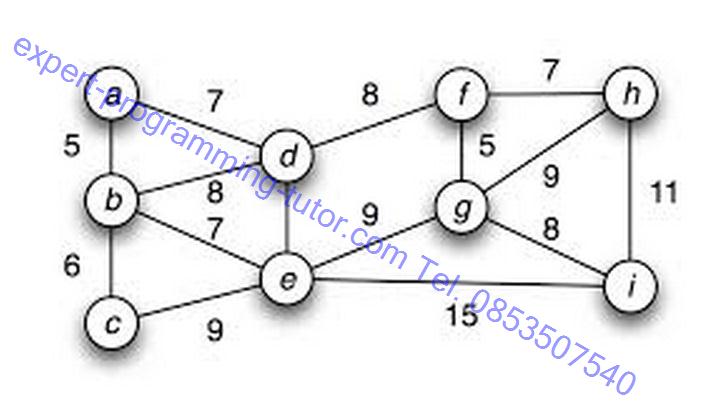รูป9-5

โค๊ดของ weighted adjacency matrix และ weighted adjacency list

weighted adjacency matrix

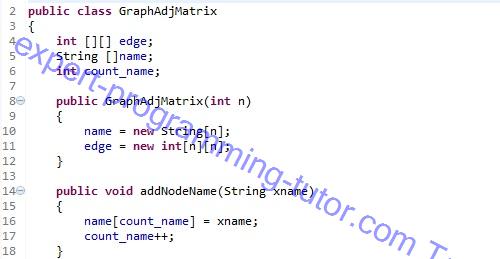รูป 9-6

บรรทัดที่ 2 : สร้างคลาสชื่อ GraphAdjMatrix

บรรทัดที่ 4 : สร้างตัวแปรที่จะใช้เก็บเอดจ์ ชื่อ edge เป็นอาร์เรย์ 2 มิติ

บรรทัดที่ 5 : สร้างตัวแปร name เป็น String สำหรับเป็นชื่อของเวอร์เท็กซ์ เมื่อทำการสร้างเวอร์เท็กซ์ใหม่

บรรทัดที่ 6 : สร้างตัวแปร count_name ไว้สำหรับการนับว่ามีเวอร์เท็กซ์กี่อันแล้ว คือเวลาทำการเพิ่มเวอร์เท็กซ์ก็ให้ตัวแปรนี้เพิ่มค่าขึ้นอีก 1

บรรทัดที่ 8 : สร้างคอนสตรัคเตอร์ของคลาส GraphAdjMatrix รับพารามิเตอร์เป็นจำนวนเต็มเข้ามา ซึ่งจำนวนเต็มนี้จะไปกำหนดค่าให้กับตัวแปรที่เป็นอาร์เรย์

บรรทัดที่ 10 : ทำการสร้าง name ขึ้นมาด้วยคำสั่ง new เอาค่าของจำนวนเต็มที่รับมาจากพารามิเตอร์มาเป็นขนาดของอาร์เรย์

บรรทัดที่ 11 : ทำการสร้าง edge ขึ้นมาด้วยคำสั่ง new เอาค่าของจำนวนเต็มที่รับมาจากพารามิเตอร์มาเป็นขนาดของอาร์เรย์

บรรทัดที่ 14 : สร้างเมท็อด addNodeName ขึ้นมา รับพารามิเตอร์เป็น String สำหรับจะใช้เป็นชื่อของเวอร์เท็กซ์

บรรทัดที่ 16 : กำหนดให้ตัวแปร name ตัวที่ count_name เก็บชื่อที่ได้มาจากพารามิเตอร์

บรรทัดที่ 17 : เพิ่มค่า count_name

รูป 9-7

บรรทัดที่ 20 : สร้างเมท็อด addEdge โดยเมื่อเป็นกราฟแบบมีน้ำหนักก็จะต้องมีการรับค่าน้ำหนักเข้ามาด้วย โดยพารามิเตอร์ของเมท็อดนี้ได้แก่ ชื่อของเวอร์เท็กซ์แรก เวอร์เท็กซ์ที่สอง และน้ำหนักของเอดจ์

บรรทัดที่ 22 : สร้างตัวแปร index_a แทนตำแหน่งดัชนีของเวอร์เท็กซ์แรก กำหนดค่าเป็น 0

บรรทัดที่ 23 : สร้างตัวแปร index_b แทนตำแหน่งดัชนีของเวอร์เท็กซ์ที่สอง กำหนดค่าเป็น 0

บรรทัดที่ 24 : สร้างลูปสำหรับหาค่าดัชนีตั้งแต่ 0 จนถึง count_name (หรือเวอร์เท็กซ์ที่มีทั้งหมด)

บรรทัดที่ 26 : สร้างเงื่อนไข ถ้ามีชื่อตำแหน่งที่ i ตรงกับ a ที่รับเข้ามา

บรรทัดที่ 28 : ให้ index_a เก็บค่า i นั้นไว้

บรรทัดที่ 29 : break จากลูป

บรรทัดที่ 32-37: ทำเหมือน24-28 แต่เป็นสำหรับ b

บรรทัดที่ 41 : ให้ edge ตำแหน่งที่ a ตำแหน่งที่ b เก็บค่าน้ำหนัก

บรรทัดที่ 42 : ให้ edge ตำแหน่งที่ b ตำแหน่งที่ a เก็บค่าน้ำหนัก (เป็น undirected ค่าไปกลับเลยเท่ากัน)

weighted adjacency list

รูป 9-8

บรรทัดที่ 4 : สร้างคลาส GraphAdjList (ในโค๊ดนี้กำหนดให้เป็นgeneric)

บรรทัดที่ 6 : เรียกคลาสลิงค์ลิสต์(เรียกจากคลาสลิงค์ลิสต์ที่มีอยู่แล้ว)

บรรทัดที่ 7 : สร้างคอนสตรัคเตอร์ของคลาส

บรรทัดที่ 9 : ให้ตัวแปร all สร้างลิงค์ลิสต์ขึ้นมา

บรรทัดที่ 12 : สร้างเมท็อด add สำหรับการเพิ่มข้อมูล

บรรทัดที่ 14 : สร้างเวอร์เท็กซ์ขึ้นมา

บรรทัดที่ 15 : เพิ่มข้อมูลด้วยการให้ตัวแปร all เรียกเมท็อด add จากคลาสลิงค์ลิสต์

รูป9-9

บรรทัดที่ 18 : สร้างเมท็อด addEdge สำหรับเพิ่มเอดจ์แบบมีน้ำหนัก

บรรทัดที่ 20 : สร้างตัวแปร index_a แทนตำแหน่งดัชนีของเวอร์เท็กซ์แรก กำหนดค่าเป็น -1

บรรทัดที่ 21 : สร้างตัวแปร index_b แทนตำแหน่งดัชนีของเวอร์เท็กซ์แรก กำหนดค่าเป็น -1

บรรทัดที่ 22 : สร้างลูปสำหรับหาค่าดัชนีตั้งแต่ 0 จนถึง count_name (หรือเวอร์เท็กซ์ที่มีทั้งหมด)

บรรทัดที่ 24 : สร้างเงื่อนไข ถ้ามีชื่อตำแหน่งที่ i ตรงกับ a ที่รับเข้ามา

บรรทัดที่ 26 : ให้ index_a เก็บค่า i นั้นไว้

บรรทัดที่ 27 : break จากลูป

บรรทัดที่ 30-35 : เหมือน 22-27

บรรทัดที่ 39 : สร้างเงื่อนไขถ้าพบว่า index_a หรือ index_b ได้ค่าเป็น -1 เท่าเดิม ถือว่าไม่เจอให้ออกจาลูป

บรรทัดที่ 41 : สร้างตัวแปร e เป็นชนิด GraphEdge

บรรทัดที่ 42 : ให้ตัวแปร from ของ e เก็บค่าที่ได้จากการ เรียกเมท็อด get ตำแหน่งของ index_a

บรรทัดที่ 43 :ให้ตัวแปร to ของ e เก็บค่าที่ได้จากการ เรียกเมท็อด get ตำแหน่งของ  index_b

บรรทัดที่ 44 : ให้ตัวแปร weight ของ e เก็บค่าของ weight

บรรทัดที่ 46-49 : เหมือน 41-44 แต่เก็บใส่ตัวแปร f

บรรทัดที่ 51 : เพิ่มข้อมูล e ใส่ลงไปใน ลิสต์ adj ที่ตำแหน่งจากการ get ของ all

บรรทัดที่ 52 : เพิ่มข้อมูล ด ใส่ลงไปใน ลิสต์ adj ที่ตำแหน่งจากการ get ของ all

            ที่ต้องเพิ่มข้อมูล e และ f ก็เพราะว่าในโหนดของลิงค์ลิสต์จะต้องเก็บชื่อเวอร์เท็กซ์และน้ำหนักไว้ในโหนด ถ้ามีโหนด 2 โหนดติดกัน ทั้งสองโหนดนั้นจะต้องเพิ่มค่าน้ำหนักลงไปทั้งสองโหนด

รูป9-10

บรรทัดที่ 5 : สร้างคลาส GraphNode

บรรทัดที่ 7 : สร้างตัวแปร data

บรรทัดที่ 8 : สร้างลิงค์ลิสต์ชื่อ adj มีชนิดข้อมูลที่เก็บเป็น GraphEdge

บรรทัดที่ 10 : สร้างคอนสตรัคเตอร์ของคลาส GraphNode

บรรทัดที่ 12 : ให้ข้อมูลเป็น null ไว้ก่อน

บรรทัดที่ 13 : adj ให้สร้างลิงค์ลิสต์ขึ้นมา

บรรทัดที่ 16 : สร้างคอนสตรัคเตอร์ของคลาส GraphNode แบบรับพารามิเตอร์ เป็น x

บรรทัดที่ 18 : ให้ x รับเข้ามาเป็นข้อมูล

บรรทัดที่ 19 : adj ให้สร้างลิงค์ลิสต์ขึ้นมา เหมือนเดิม

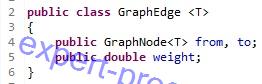รูป9-11

บรรทัดที่ 2 : สร้างคลาส GraphEdge สำหรับเป็นเอดจ์ในกราฟ

บรรทัดที่ 4 : สร้างตัวแปรชนิด GraphNode คือ from และ to

บรรทัดที่ 5 : สร้างตัวแปร weight สำหรับเป็นน้ำหนัก