Merge sort เป็นอัลกอริทึมแบบแบ่งแยกและเอาชนะ (divide and conquer algorithm) ก็คือมีการแบ่งแยก โดยแบ่งข้อมูลออกเป็นสองส่วนจากนั้นให้ recursive เรียกตัวเอง ต่อมาเอาชนะเป็นการเอาแต่ละส่วนมาพิจารณารวมกันจนได้เป็นส่วนใหญ่ที่เรียงลำดับเรียบร้อยแล้ว โดยส่วนที่เอามาพิจารณาต้องเรียงลำดับแล้วด้วย สมมติว่ามีข้อมูลอยู่ n ตัว เวลาการทำงานก็จะเป็น T(n) ซึ่งการคำนวณหาเวลาก็หาได้จาก master’s method คือ T(n) = 2T(n/2) + n 

            การทำงานของ merge sort เป็นไปอย่างรวดเร็วเพราะในกรณีแย่สุดก็ยังทำงานแค่ O(n log n) นอกจากนี้ยังสามารถทำได้ทั้งแบบบนลงล่าง (Top-down) และแบบล่างขึ้นบน (Bottom-up) 

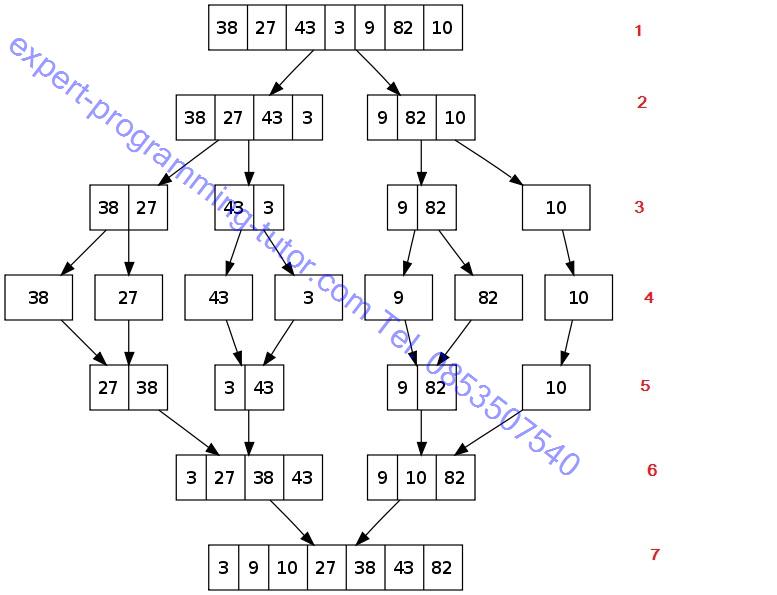รูป1-7

            บรรทัดที่ 1 มีข้อมูลอยู่หนึ่งชุด แบ่งออกมาครึ่งหนึ่งแล้วแบ่งอีกครึ่งหนึ่งจนได้ข้อมูลเดี่ยวในบรรทัดที่ 4 ค่อยๆ merge ที่ข้อมูลกลับเข้ามาโดยเรียงให้เป็นลำดับ รวมกันเรื่อยๆจนได้บรรทัดที่ 7 ก็จะได้ข้อมูลชุดเดิมที่เอาเข้ามาแต่เรียงลำดับแล้ว

ประสิทธิภาพการทำงานของ การเรียงลำดับแบบ Merge

ประสิทธิภาพการทำงานเมื่อเกิดกรณีแย่สุด O(n log n)

ประสิทธิภาพการทำงานเมื่อเกิดกรณีทั่วไป O(n log n)

ประสิทธิภาพการทำงานเมื่อเกิดกรณีดีที่สุด O(n log n) โดยทั่วไป หรือ O(n) เมื่อใส่เงื่อนไขพิเศษ

Merge sort source code

รูป1-8

บรรทัดที่  59 : สร้างเมท็อด mergeSort รับอินพุทเป็น อาร์เรย์ และตัวแปรตำแหน่งซ้ายสุด(l) ตัวแปรตำแหน่งขวาสุด(r)

บรรทัดที่  60 : ถ้ารับเข้ามาแล้วตำแหน่ทางซ้ายมากกว่าตำแหน่งทางขวาให้คืนค่าออกไป

บรรทัดที่  61 : สร้างตัวแปร m เพื่อหาตำแหน่งตรงกลาง โดยตำแหน่งตรงกลางจะได้จากการเอาตำแหน่งซ้ายกับขวามาบวกกันแล้วหารสอง

บรรทัดที่  63 : เรียกซ้ำตัวเองโดยให้อินพุทขวาสุดเป็นตรงกลางแล้วหาค่ากลาง เรียกซ้ำแบ่งไปเรื่อยๆ

บรรทัดที่  64 :เรียกซ้ำตัวเองอีกอัน โดยให้อินพุทซ้ายสุดเป็นค่าถัดจากตรงกลางมาหนึ่งค่าแล้วหาค่ากลาง เรียกซ้ำแบ่งไปเรื่อยๆ

บรรทัดที่  69-70 : เอาตัวน้อยช่อง i (ช่องซ้ายสุดถึงตรงกลาง) ไปเก็บใน k เพิ่มค่าตรวจสอบตัวถัดไป

บรรทัดที่  73-74 : เอาตัวน้อยช่อง j (ช่องตรงกลางไปถึงขวา) ไปเก็บใน k เพิ่มค่าตรวจสอบตัวถัดไป

บรรทัดที่  78-79 : ถ้าตัวซ้ายมากกว่าตัวตรงกลางแล้วให้ออกจากลูป

บรรทัดที่  92-93 : เอาค่าที่อยู่ใน temp[i] มาใส่ a[i] ให้เป็นลำดับ

การเรียงลำดับแบบเร็ว (Quick Sort)

            การเรียงลำดับแบบเร็ว คือโดยส่วนใหญ่จะสามารถเรียงลำดับได้เร็วกว่าแบบอื่นในบรรดากลุ่ม O(n log n) แต่ก็มีกรณีเลวร้ายสุดคือ O(n) แต่ก็ไม่ได้เกิดบ่อยๆ โดย quick sort ก็เป็นอัลกอริทึมแบบแบ่งแยกและเอาชนะเหมือน merge sort แต่ก็ไม่เหมือนกันตรงที่ quick sort แบ่งอาร์เรย์ใหญ่ออกเป็นสองอาร์เรย์ย่อยแล้วค่อยๆทำจากสองอาร์เรย์ย่อย โดยจะซุ่มหาตำแหน่งกลางซึ่งอาจจะไม่ได้อยู่ตรงกลางก็ได เรียกว่า pivot ในการเปรียบเทียบ เพื่อทำการสลับให้ค่าที่น้อยกว่าจุดที่เลือกไปอยู่ทางซ้ายของตำแหน่งกลาง recursive ซ้ำจนทั้งหมดอยู่ในตำแหน่งที่ถูกต้อง

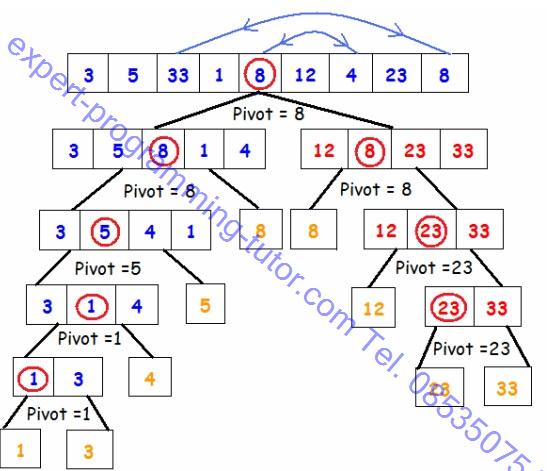รูป1-9

บรรทัดแรกได้อาร์เรย์มาหนึ่งชุด ได้ pivot เป็น 8 อันที่น้อยกว่า 8 ก็มาเป็นอาร์เรย์ทางซ้ายสีน้ำเงิน มากกว่าหรือเท่ากับ 8 อยู่ทางขวาสีแดง เลือก pivot ซ้ำในแต่ละข้างจนเหลือเป็นข้อมูลเดียวเอาข้อมูลไล่จากซ้ายไปขวาจะได้ข้อมูลชุดใหม่ที่เรียงเรียบร้อยแล้ว

ประสิทธิภาพการทำงานของ การเรียงลำดับแบบ quick

ประสิทธิภาพการทำงานเมื่อเกิดกรณีแย่สุด O(n)

ประสิทธิภาพการทำงานเมื่อเกิดกรณีทั่วไป O(n log n)

ประสิทธิภาพการทำงานเมื่อเกิดกรณีดีที่สุด O(n log n)

Quick sort source code

รูป1-10

บรรทัดที่  99 : สร้างเมท็อด quicksort รับอินพุทเป็น อาร์เรย์ และตัวแปรตำแหน่งซ้ายสุด(l) ตัวแปรตำแหน่งขวาสุด(r)

บรรทัดที่  101 : ถ้ารับเข้ามาแล้วตำแหน่งทางซ้ายมากกว่าตำแหน่งทางขวาให้คืนค่าออกไป

บรรทัดที่  102 : สร้างตัวแปร temp เก็บค่าของข้อมูลตัวซ้ายสุด

บรรทัดที่  103 : สร้างตัวแปร i โดยให้ i เริ่มที่ตำแหน่งซ้ายสุด

บรรทัดที่  104 : สร้างตัวแปร j โดยให้ j เริ่มที่ตำแหน่งขวาสุดบวก1

สิ่งที่จะทำต่อไปนี้คือ

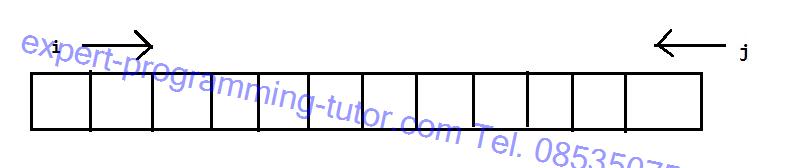รูป1-11

            สร้าง i และ j สำหรับเลื่อนข้อมูลให้ i เลื่อนไปทางขวา ส่วน j เลื่อนไปทางซ้ายเลื่อนจนกระทั่ง i กับ j มาพบกันตรงกลาง โดยถ้าพบว่า ตำแหน่งของ i มีข้อมูลที่มีค่ามากกว่าตำแหน่งของ j ให้สลับข้อมูลสองตัว ส่วนข้อมูลเท่ากับไม่ต้องสลับที่กันเพราะไม่ได้อะไร

บรรทัดที่  106 : วนลูปตราบเท่าที่ i ยังน้อยกว่า j

บรรทัดที่  108-113 : ถ้า temp ยังน้อยกว่าตัวตำแหน่งที่ j ให้ j เลื่อนมาทางซ้ายและ i เลื่อนไปทางขวา

บรรทัดที่  115-118 : ถ้าตำแหน่งที่มีข้อมูลน้อยกว่า temp ให้เลื่อน i ไปทางขวา แต่ถ้า i เท่ากับ r ก็ break

บรรทัดที่  120-124 : ตอนที่ i ยังน้อยกว่า j ให้ สลับตำแหน่งกัน

บรรทัดที่  132 : เรียกซ้ำการทำงาน

บรรทัดที่  133 : เรียกซ้ำการทำงาน

การเรียงลำดับแบบเชลล์ (Shell Sort)

            เป็นการเรียงลำดับที่ปรับปรุงมาจาก insertion sort อีกที เพราะ insertion sort ช้าตรงที่ต้องเลื่อนข้อมูลออกไปทีละช่องๆ เชลล์ซอร์ทก็เปลี่ยนเป็นเลื่อนทีละ h ช่องแทน ดูได้จากรูปข้างล่าง

            มีข้อมูลอยู่หนึ่งชุด

                                                                         รูป1-12          

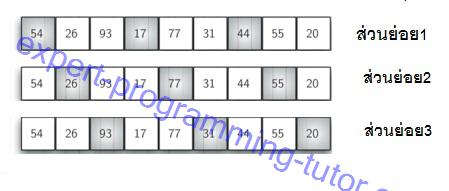รูป1-13

                   แบ่งข้อมูลเป็นสามส่วน โดยจะเลือกตามรูปข่างล่างโดยเสมือนว่าตัวที่ห่างกันอยู่ติดกัน

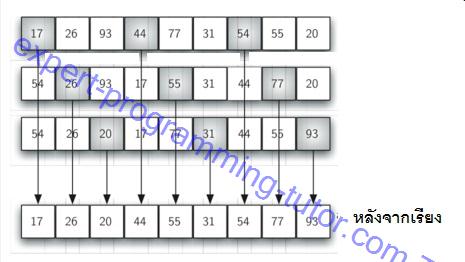รูป1-14

            เมื่อข้อมูลอยู่ติดกันแล้วให้ทำการเรียงแบบ insertion sort ปกติ ก็จะได้ข้อมูลที่เรียงแล้ว

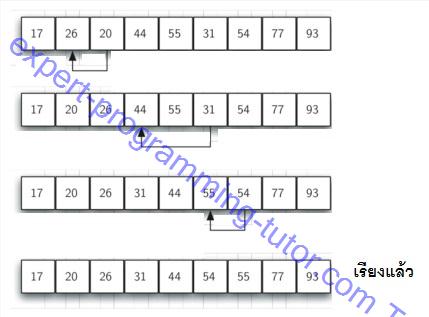รูป1-15

Shell sort source code

รูป1-16

บรรทัดที่ 167 : สร้างคลาส shellSort รับอินพุทเป็นอาร์เรย์ a

บรรทัดที่ 169-170 : สร้างตัวแปล h สำหรับการเลือกช่องว่างว่าจะให้ห่างกันกี่ตัว

บรรทัดที่ 171 : ให้ลดลงทีละหารสอง

บรรทัดที่ 173: วนลูปขนาดเท่ากับ h

บรรทัดที่ 175-183: เป็นการ insertion