 รูป6-6
รูป6-6
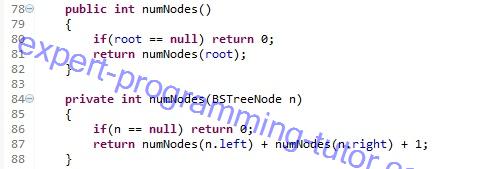
คลาส numNodes สำหรับการตรวจสอบว่าในต้นไม้นั้นมีโหนดอยู่ทั้งหมดกี่โหนด ถ้าต้นไม่มีสักโหนดก็ถือว่ามี 0 โหนดคือค่า 0 แต่ถ้าไม่ใช่ 0 วิธีหาจำนวนโหนดคือเอา ราก(1 โหนด) +จำนวนโหนดย่อยทางซ้ายทั้งหมด + จำนวนโหนดย่อยทางขวาทั้งหมด
บรรทัดที่ 78 : สร้างเมท็อด ชื่อ numNodes
บรรทัดที่ 80 : ถ้ารากเท่ากับ null หมายถึงยังไม่มีรากก็เท่ากับยังไม่มีข้อมูลตัวอื่นๆทั้งหมด ให้คืนค่าเป็น 0
บรรทัดที่ 81 : แต่ถ้ามีรากอยู่ให้เรียก numNodes ที่รับพารามิเตอร์เป็นรากเข้ามา
บรรทัดที่ 84 : สร้างเมท็อด ชื่อ numNodes เป็น private สำหรับให้เมท็อดของคลาสนี้เรียกเท่านั้น
บรรทัดที่ 86 : ตรวจสอบอีกครั้งว่ารากเท่ากับ null หรือไม่
บรรทัดที่ 87 : คืนค่า + จำนวนโหนดย่อยทางซ้าย + จำนวนโหนดย่อยทางขวา เพื่อหาค่าโหดนทั้งหมด
 รูป6-7
รูป6-7
เมท็อด height สำหรับหาความสูงของต้นไม้โดยความสูงของต้นไม้คือความสูงตั้งแต่รากไปจนถึงใบที่ลึกที่สุด วิธีหาก็คือไปหาจากต้นไม้ย่อยทางซ้ายกับต้นไม้ย่อยทางขวา หาระหว่างสองอันนี้มีอันไหนยาวสุดแล้วเอามาบวกเพิ่มอีกหนึ่ง บวกรากเข้าไปด้วย ดังนั้นถ้าต้นไม้มีแต่รากจะถือว่าสูง 0 แต่ถ้าต้นไม้ว่างไม่มีข้อมูลจะสูงเป็น -1
บรรทัดที่ 100 : สร้างเมท็อด height
บรรทัดที่ 102 : ตรวจสอบว่ารากเป็น null หรือเปล่า ถ้าใช่ให้คือค่าเป็น -1
บรรทัดที่ 103 : สมมติไม่ null ให้เรียก height อีกตัวหนึ่ง
บรรทัดที่ 106 : สร้างเมท็อด height ที่เป็น private รับพารามิเตอร์เป็นรากเข้ามา
บรรทัดที่ 108 : ตรวจสอบซ้ำว่ารากเป็น null หรือเปล่า ถ้าใช่ให้คือค่าเป็น -1
บรรทัดที่ 109 : สร้างตัวแปล l สำหรับหาความสูงของข้อมูลทางซ้าย
บรรทัดที่ 110 : สร้างตัวแปล r สำหรับหาความสูงของข้อมูลทางขวา
บรรทัดที่ 111 : ตรวจสอบด้วย if-else ว่า ต้นไม้ทางซ้ายมากกว่าต้นไม้ทางขวาหรือไม่ ถ้าใช่ให้เลือกทางซ้าย ถ้าไม่ใช่ให้เลือกทางขวาแล้วเอาตัวที่ได้มา +1 เป็นความสูงของต้นไม้
 รูป6-8
รูป6-8
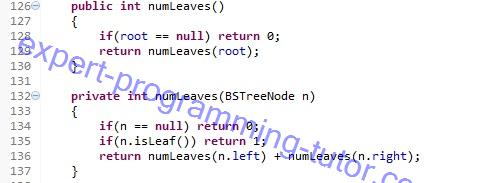
เมท็อด numLeaves สำหรับการหาใบทั้งหมดในต้นไม้ ใบคือโหนดที่ไม่มีลูกซ้ายขวา ใบรวมกันคือใบลูกซ้ายบวกกับใบลูกขวา ถ้าต้นไม้ว่างคืนค่า 0 คือไม่มีสักใบ ถ้ามีรากโหนดเดียวถือว่ามี 1 ใบ ถ้ามีมากกว่านั้นก็หาแล้วเอามาบวกกัน
บรรทัดที่ 126 : สร้าง numLeaves สำหรับการหาจำนวนใบทั้งหมด
บรรทัดที่ 128 : ถ้ารากเป็น null คือทั้งต้นไม้ไม่มีข้อมูลเลยให้คืนค่าเป็น 0 เลย แสดงว่าไม่มีสักใบ
บรรทัดที่ 129 : ถ้ารากไม่ null ให้เรียกเมท็อด numLeaves อีกอัน
บรรทัดที่ 132 : สร้าง numLeaves รับพารามิเตอร์เป็นโหนดราก
บรรทัดที่ 134 : ตรวจซ้ำถ้ารากเป็น null คือทั้งต้นไม้ไม่มีข้อมูลเลยให้คืนค่าเป็น 0
บรรทัดที่ 135 : ตรวจว่าตัวรากนั้นมีลูกหรือเปล่าด้วยเมท็อด isLeaf ว่ามีโหดนลูกซ้ายขวาไหม ถ้าไม่มีโหดนลูกซ้ายขวาให้คืนค่าเป็น 1 เพราะมีรากอันเดียวในต้นไม้
บรรทัดที่ 136 : ถ้าไม่ใช่กรณีข้างบนให้หาจำนวนใบทั้งหมดแล้วเอามาบวกกัน
การลบข้อมูลในต้นไม้
การลบโหนดในต้นไม้ซับซ้อนกว่าการลบข้อมูลในอาร์เรย์ลิสต์และลิงค์ลิสต์ สมมติว่าต้องการลบโหนดๆหนึ่งที่มีลูกแค่ข้างเดียวก็จะไม่ซับซ้อนเท่าไหร่
 รูป6-9
รูป6-9
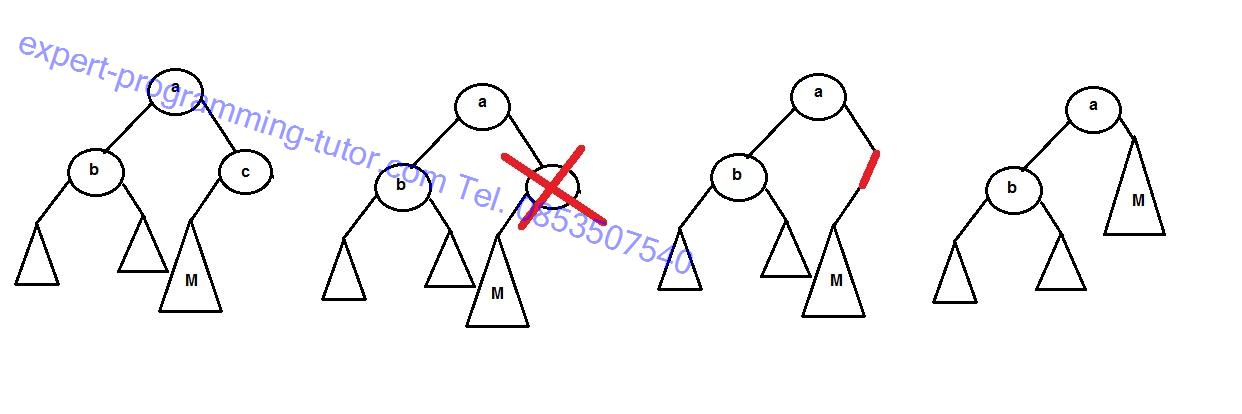
จากภาพต้องการลบโหนด c ซึ่งโหดน c มีลูกอยู่ฝั่งเดียวคือกลุ่ม M ถ้าตัด c ออกไปแม้ M จะน้อยกว่า c แต่ก็ยังมีค่ามากกว่า โหนดราก a อยู่ดีเพราะกลุ่ม M อยู่ในกลุ่มทางขวามือของโหนดราก พอเอา c ออกก็สามารถเอา M มาแปะไว้ทางขวามือของรากได้เลย
 รูป6-10
รูป6-10
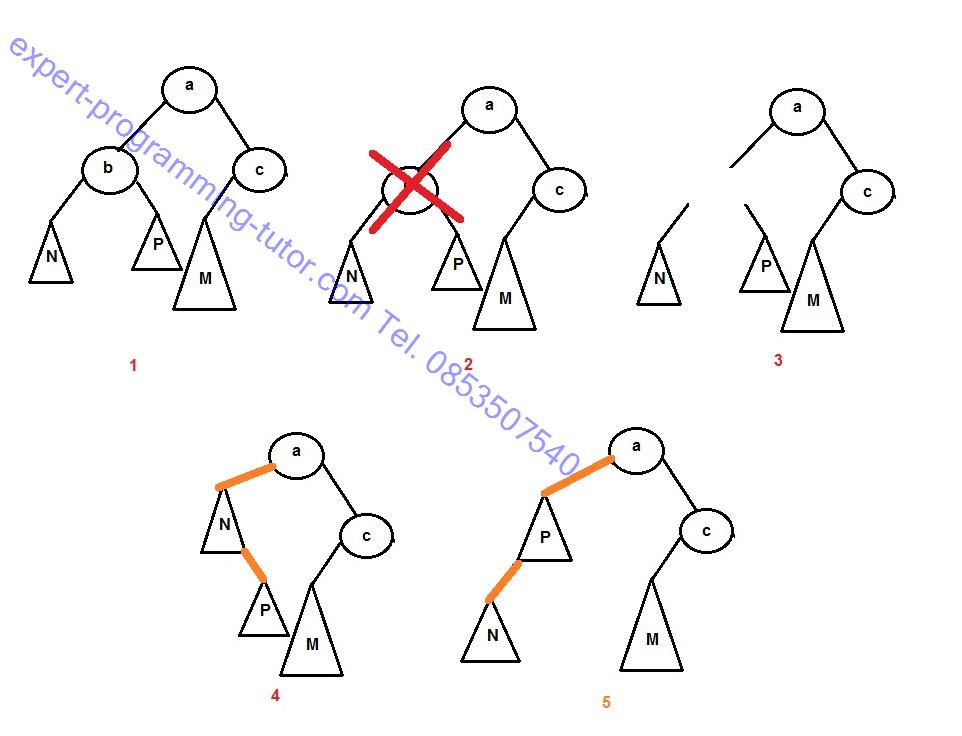
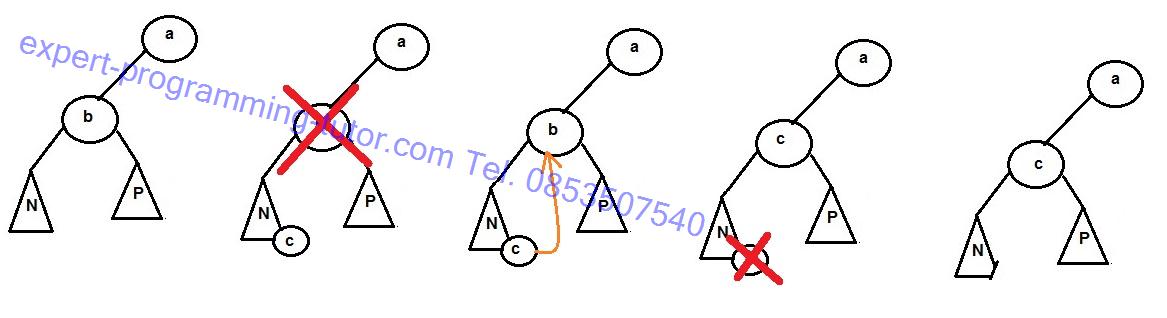
แต่ถ้าสมมติไม่ได้ต้องการลบ c แต่อยากลบ b ที่มีลูกอยู่ทั้งสองข้าง พอรูปที่ 3 จะต้องเลือกว่าเมื่อไม่มี b แล้วจะให้ N และ P อยู่ตำแหน่งใด คือจะให้ 4 คือเอา N ขึ้นก่อนแล้วเอา P มาต่อ เพราะ P มากกว่า b และ b มากกว่า N P ก็ต้องมากกว่า N ก็ให้เอา P มาอยู่ทางขวาของ N หรือตะสลับกันดังรูป 5 ก็ได้ เพราะ N น้อยกว่า P ก็เอา N มาอยู่ข้างซ้ายของ P แต่ปัญหาคือเวลาเรา “ลบ” ก็ควรจะหมายถึงทำให้น้อยลง แต่การลบแบบในรูปเป็นการทำให้ต้นไม้สูงขึ้นเวลาค้นหาก็ต้องใช้เวลามากขึ้นมันจึงไม่เป็นวิธีที่ดีเท่าไหร่
อีกวิธีหนึ่งก็คือการหาตัวแทนสลับที่กัน คือเช่นถ้าจะลบ b ก็หาตัวที่มากสุดของ N ไปอยู่แทนตำแหน่ง b หรือไม่งั้นก็เอาตัวที่น้อยสุดของ P ไปไวที่ตำแหน่ง b
 รูป6-11
รูป6-11
ภ้าใช้วิธีนี้ก็เลือกเอาตัวที่มากสุดฝั่งซ้ายไปแทน b เพราะมากที่สุดฝั่งซ้ายหมายความว่าตัวที่ไม่ใช่ตัวมากสุดทุกตัวจะต้องน้อยกว่าตัวนี้แน่ๆ เช่น c มากสุดทุกตัวที่ไม่ใช่แต่อยู่ฝั่งซ้ายจะต้องน้อยกว่า c แต่เนื่องจาก c อยู่ในฝั่งซ้าย ดังนั้นถึงจะมากที่สุดแต่ก็ต้องน้อยกว่าทุกๆตัวของฝั่งขวา เพราะตัวฝั่งขวามากกว่า b และ b มากกว่า c จึงเอา c ไปแทนได้ และในทางกลับกันคือจะเลือกตัวน้อยสุดของฝั่งขวาก็ได้
 รูป3-12
รูป3-12
บรรทัดที่ 139 : สร้างเมท็อด remove สำหรับการลบข้อมูล
บรรทัดที่ 141 : ตรวจสอบว่าถ้ารากว่าง ซึ่งหมายถึงต้นไม้ว่าง ให้คืนค่าออกไปเพราะไม่มีอะไรจะลบ
บรรทัดที่ 142 : เรียกเมท็อดสำหรับลบ
บรรทัดที่ 145 : สร้างเมท็อด remove สำหรับการลบข้อมูลแต่รับพารามิเตอร์เป็นรากกับข้อมูลที่จะลบ
บรรทัดที่ 147 : ตรวจสอบซ้ำว่าถ้าถ้ารากว่าง ให้คืนค่าออกไป
บรรทัดที่ 148-150 : ถ้าข้อมูลที่รากมากกว่าข้อมูลที่จะลบ ให้ไปหาข้อมูลที่จะลบจากลูกทางซ้ายของราก
บรรทัดที่ 152-154 : ถ้าข้อมูลที่รากน้อยกว่าข้อมูลที่จะลบ ให้ไปหาข้อมูลที่จะลบจากลูกทางขวาของราก
บรรทัดที่ 158-160: ถ้าข้อมูลทางซ้ายหรือทางขวาของรากไม่มี (รากมีลูกข้างเดียว) ตรวจสอบว่าลูกซ้ายว่างใช่หรือไม่ ถ้าใช่ก็ไปลบทางขวา แต่ถ้าทางขวาว่างก็ไปลบทางซ้าย สลับกัน
บรรทัดที่ 164 : ถ้ามีลูกทั้งสองข้าง ให้สร้างโหนด m ขึ้นมาซึ่งให้ m เป็นลูกทางขวา
บรรทัดที่ 165-167 : หาค่าน้อยสุดในกลุ่มโหนด m โดยการให้หาลูปทางซ้ายของ m ไปเรื่อยๆ
บรรทัดที่ 169 : เอาค่า m ที่ได้ไปแทนที่ตัวที่จะลบ
บรรทัดที่ 170 : ลบ m ออกไป
Tag ที่น่าสนใจ: binary_search_tree data_structure node_manipulation tree_height leaf_nodes node_removal
หากมีข้อผิดพลาด/ต้องการพูดคุยเพิ่มเติมเกี่ยวกับบทความนี้ กรุณาแจ้งที่ http://m.me/Expert.Programming.Tutor
085-350-7540 (DTAC)
084-88-00-255 (AIS)
026-111-618
หรือทาง EMAIL: NTPRINTF@GMAIL.COM

Copyright (c) 2013 expert-programming-tutor.com. All rights reserved. | 085-350-7540 | 084-88-00-255 | ntprintf@gmail.com
