Binary search tree (BST) หรือชื่อภาษาไทยว่าต้นไม้ทวิภาค เป็นการจัดเก็บข้อมูลรูปแบบหนึ่งที่มีประสิทธิภาพโดยเฉพาะการเพิ่ม ลบ ค้นหา หาตัวมากสุดหรือตัวน้อยสุด มีลักษณะการเก็บข้อมูลเป็นโหนด (Node) คล้ายกับ Linked List แต่ไม่ได้เก็บเป็นลักษณะเส้นตรงเหมือนกัน เพราะ BST จะเก็บข้อมูลในลักษณะที่ว่าข้อมูลทางขวาจะมากกว่าตัวตรงกลางและตัวทางซ้าย แต่ละโหนดมีลูกได้ไม่เกินสองโหนด โหนดลูกซ้ายต้องน้อยกว่าโหนดพ่อแม่ และโหนดลูกขวาต้องมากกว่าโหนดพ่อแม่ การเรียงในลักษณะนี้ทำให้ BST ได้เปรียบในเรื่องของการค้นหาข้อมูลเพราะข้อมูลที่เก็บไว้ได้อยู่รูปแบบที่ง่ายต่อการค้นหาอยู่แล้ว
 รูป6-1
รูป6-1
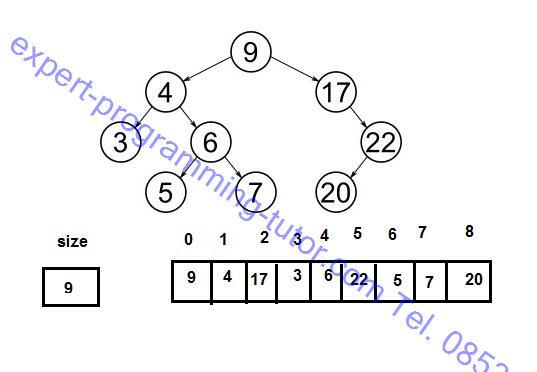
ลักษณะของ BST
- ลูกทางซ้ายของโหนดจะมีค่าน้อยกว่าโหนด 4 น้อยกว่า 9 และ 5 น้อยกว่า 6
- ลูกทางขวาของโหนดจะมีค่ามากกว่าโหนด 17 มากกว่า 9 และ 6 มากกว่า 4
- แต่ละโหนดลูกได้สองตัว (มีโครงสร้างต้นไม้ที่มีลูกได้มากกว่า 3 โหนด แต่ไม่ได้เรียก BST)
- ต้องไม่มีข้อมูลซ้ำกัน
- สามารถค้นหาข้อมูลได้เร็วถ้าต้นไม้มีลักษณะสมดุลกัน
- การเพิ่มและการลบข้อมูลมีประสิทธิภาพ
การสร้างต้นไม้
การสร้างต้นไม้ ไม่จำเป็นต้องเก้บเลขจำนวนเต็มจะเก็บอย่างอื่นก็ได้ วิธีการสร้างต้นไม้อย่างง่ายเลยก็คือสร้างโหนดเก็บข้อมูลและโหนดนั้นก็ต้องมีตัวชี้ลูกซ้ายและตัวชี้ลูกขวา ถ้าข้างไหนไม่มีลูกก็ให้เป็น null ไป และต้นไม้จะมีโหนดแรกสุดเลยเรียกว่าราก (root) ซึ่งโหนดนี้จะเป็นโหนดตั้งต้นที่ชี้ไปโหนอื่นๆ ดังนั้นขั้นตอนแรกของการสร้างต้นไม้ก็ต้องสร้างโหนดขึ้นมาก่อน
 รูป6-2
รูป6-2
บรรทัดที่ 5 : สร้างคลาสโหนดสำหรับต้นไม้ ตั้งชื่อว่า BSTreeNode
บรรทัดที่ 7 : สร้างตัวแปร data เก็บข้อมูลเป็นจำนวนเต็ม
บรรทัดที่ 8 : สร้างตัวแปร left เป็นชนิด BSTreeNode สำหรับเป็นตัวชี้ลูกทางซ้าย
บรรทัดที่ 9 : สร้างตัวแปร right เป็นชนิด BSTreeNode สำหรับเป็นตัวชี้ลูกทางขวา
บรรทัดที่ 11 : สร้างคอนสตรัคเตอร์ของคลาส BSTreeNode สำหรับการกำหนเค่าเริ่มต้นให้ตัวแปรของคลาส
บรรทัดที่ 13 : ตัวแปร data ใส่ค่าเริ่มต้นเป็น 0
บรรทัดที่ 14 : ตัวแปร left ใส่ค่าเริ่มต้นเป็น null
บรรทัดที่ 15 : ตัวแปร right ใส่ค่าเริ่มต้นเป็น null
บรรทัดที่ 18 : สร้างคอนสตรัคเตอร์ของคลาส BSTreeNode โดยที่คอนสตรัคเตอร์นี้รับพารามิเตอร์เป้นข้อมูลจำนวนเต็มเข้ามาหนึ่งตัวเพื่อเป็นค่าให้กับด้วยแปร data
 รูป 6-3
รูป 6-3
บรรทัดที่ 24 : สร้างเมท็อด isLeaf เป็น boolean สำหรับคืนค่าว่าตัวนั้นๆเป็นโหนดใบหรือไม่ โหนดใบหายถึงโหนดที่ไม่มีลูกซ้ายหรือขวาต่ออกไปจากตัวมันเอง โดยที่โหนดใบไม่ใช่โหนดราก
บรรทัดที่ 26: คืนค่าถ้าข้อมูลการโยงซ้ายขวาไม่มีการชี้
เมท็อดใน BST
Int numNodes(Node r) จำนวนปมของต้นไม้
Int height(Node r) หาความสูงของต้นไม้
Int numLeaves(Node) หาจำนวนของใบในต้นไม้
ชนิดข้อมูล getMin หาค่าของข้อมูลน้อยที่สุด
ชนิดข้อมูล getMax หาค่าของข้อมูลมากที่สุด
void add เพิ่มข้อมูลลงต้นไม้
void romove ลบข้อมูลออกจากต้นไม้
 รูป6-4
รูป6-4
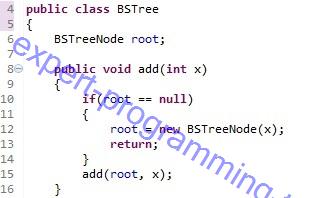
บรรทัดที่ 4 : สร้างคลาสใหม่ที่เป็นต้นไม้จริงๆให้ชื่อว่า BSTree
บรรทัดที่ 6 : สร้างโหนดรากชื่อ root ขึ้นมาเป็นข้อมูลชนิด BSTreeNode
เมท็อด add สำหรับเพิ่มข้อมูลลงในต้นไม้ การเพิ่มข้อมูลลงในต้นไม้ไม่หมือนกับพวกอาร์เรย์เพราะเวลาเพิ่มลงไปข้อมูลต้องไปลงตำแหน่งตามกฎของต้นไม้
บรรทัดที่ 8 : สร้างเมท็อด add รับพารามิเตอร์เป็นจำนวนเต็ม
บรรทัดที่ 10 : ก่อนจะทำการเพิ่มข้อมูลลงในต้นไม้ต้องทำการตรวจสอบก่อนว่าในต้นไม้นั้นมีโหนดรากอยู่แล้วหรือไม่
บรรทัดที่ 12-13 : ถ้าไม่มีโหนดรากให้สร้างโหนดรากขึ้นมาก่อน แล้วเพิ่มข้อมูลลงในโหนดราก จากนั้นคืนค่าออกไปจบการทำงานได้โหนดรากขึ้นมา
บรรทัดที่ 15 : สมมติมีโหนดรากอยู่แล้วให้เรียกการทำงานของฟังก์ชัน add ที่รับพารามิเตอร์เป็นรากและข้อมูลเข้า (เรียกว่า recursive function)
 รูป6-5
รูป6-5
บรรทัดที่ 18 : สร้างเมท็อด add รับพารามิเตอร์เป็นรากและข้อมูล ตั้งค่าเป็น private สำหรับให้เมท็อด add แรกเรียกได้เท่านั้น
บรรทัดที่ 20 : ตรวจสอบอีกครั้งว่าหากยังไม่มีโหนดรากให้คืนค่าออกไป
บรรทัดที่ 21 : ตรวจสอบว่าข้อมูลของรากมีค่ามากกว่าข้อมูลที่เข้ามาหรือไม่
บรรทัดที่ 23 : ถ้าใช่ ข้อมูลที่เข้ามาใหม่จะต้องเป็นลูกทางซ้ายของราก ดังนั้นต้องตรวจสอบว่ามีโหนดทางซ้ายอยู่แล้วหรือไม่
บรรทัดที่ 25-26 : ถ้ายังไม่มีให้สร้างโหนดแล้วเพิ่มข้อมูลลงไปในโหนดนั้น จากนั้นจบการทำงาน
บรรทัดที่ 28 : หากพบมีโหนดทางซ้ายอยู่ก่อนแล้วให้เรียก add ใหม่คราวนี้ตั้งข้อมูลโหนดทางซ้ายเป้นรากแทนแล้วเอาข้อมูลที่เอาเข้ามาไปเทียบใหม่ว่ามากหรือน้อยกว่าข้อมูลโหนดทางซ้ายนั้น
บรรทัดที่ 30 : ถ้าเกิดว่าข้อมูลที่เข้ามามีค่ามากกว่าราก ข้อมูลจะต้องไปอยู่ทางขวาของราก
บรรทัดที่ 32 : ตรวจสอบเหมือนเดิมว่าทางขวามีโหนดอยู่ก่อนแล้วหรือไม่
บรรทัดที่ 34-35 : ถ้าไม่มีโหนดทางขวาให้สร้างโหนดขึ้นมาแล้วทำการเพิ่มข้อมูลลงไปจากนั้นจบการทำงาน
บรรทัดที่ 37 : หากมีโหดนอยู่ก่อนแล้วให้เอาโหดนที่เจอเป้นรากแล้วเรียกซ้ำ add อีกครั้ง
Tag ที่น่าสนใจ: binary_search_tree data_structure nodes linked_list tree_structure insertion deletion searching recursive_function root_node leaf_nodes data_organization bst_methods node_height min/max_value efficiency
หากมีข้อผิดพลาด/ต้องการพูดคุยเพิ่มเติมเกี่ยวกับบทความนี้ กรุณาแจ้งที่ http://m.me/Expert.Programming.Tutor
085-350-7540 (DTAC)
084-88-00-255 (AIS)
026-111-618
หรือทาง EMAIL: NTPRINTF@GMAIL.COM

Copyright (c) 2013 expert-programming-tutor.com. All rights reserved. | 085-350-7540 | 084-88-00-255 | ntprintf@gmail.com
