Recursive ใน JAVA สร้าง Sierpinski triangle 
Tuesday, December 31, 2013, 12:55 PM
Posted by Administrator

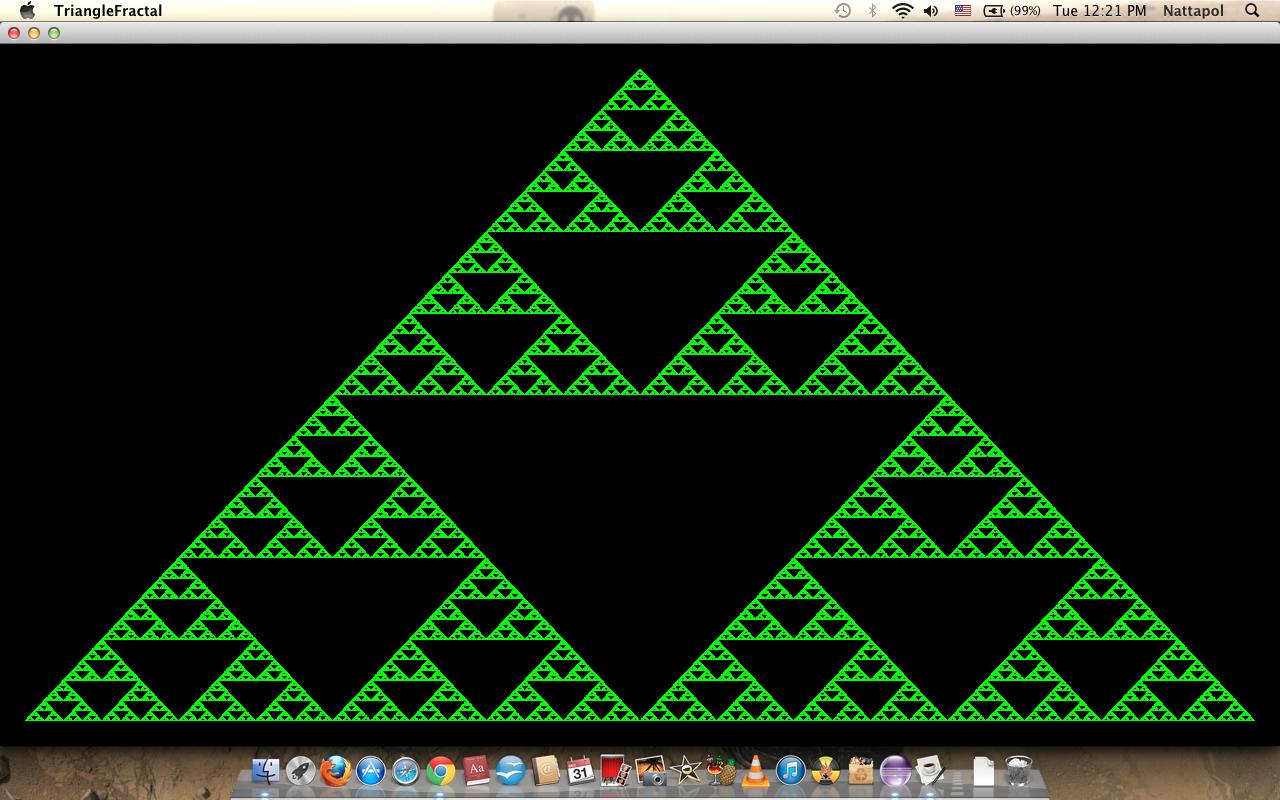
fractal Sierpinski triangle โดยใช้ภาษา JAVA




import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.Toolkit;

import javax.swing.JFrame;
import javax.swing.JPanel;

public class TriangleFractal extends JPanel
{
	public TriangleFractal()
	{
		setBackground(Color.black);
	}
	public void paint(Graphics g)
	{
		super.paint(g);
		for(int i=0;i< 1000000;i++)
		{
			draw( g,  50, getWidth() - 50, getHeight()-50, getWidth()/2, getHeight()-25);
		}
	}

	public void draw(Graphics g, double n,double w,double h,double x,double y)
	{
		if(n ==0)
		{
			g.setColor(Color.green);
			g.fillRect((int)(x+Math.random()*w-w/2),(int) (y+Math.random()*h-h/2), 1, 1);
			return;
		}
		
		double r= Math.random();
		if(r < 1.0/3.0)
		{
			y = y - h /2;
			
		}
		else if(r < 2.0/3.0)
		{
			x = x - w/4;
		}
		else
		{
			x = x + w/4;
		}
		draw( g,  n-1, w/2, h/2, x, y);
	}
	public static void main(String[] args)
	{
		JFrame fnt = new JFrame();
		
		fnt.add(new TriangleFractal());
		fnt.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
		Dimension screenSize = Toolkit.getDefaultToolkit().getScreenSize();
		double width = screenSize.getWidth();
		double height = screenSize.getHeight();
		fnt.setSize((int)width, (int)height);
		fnt.setVisible(true);
		
	}

}



 

จำนวนครั้งของ recursive n=1



จำนวนครั้งของ recursive n=2



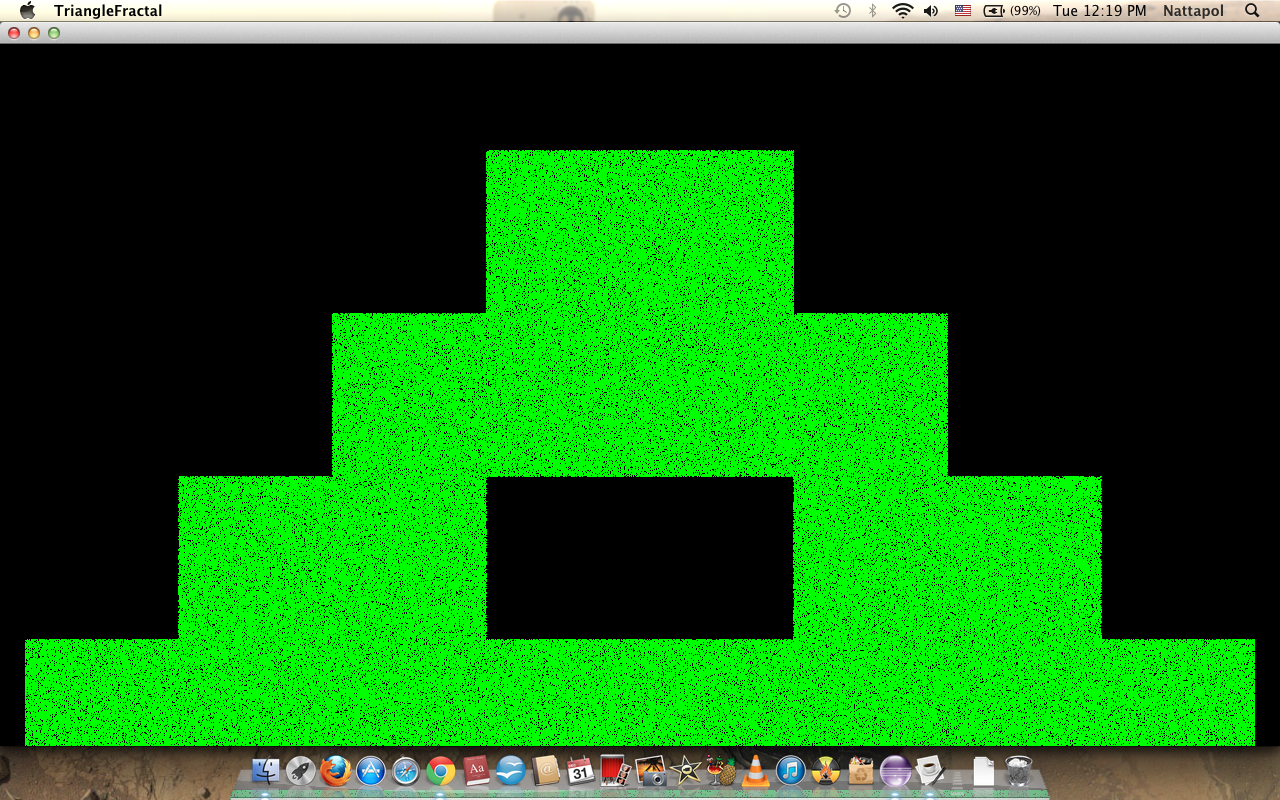
จำนวนครั้งของ recursive n=3



จำนวนครั้งของ recursive n=4



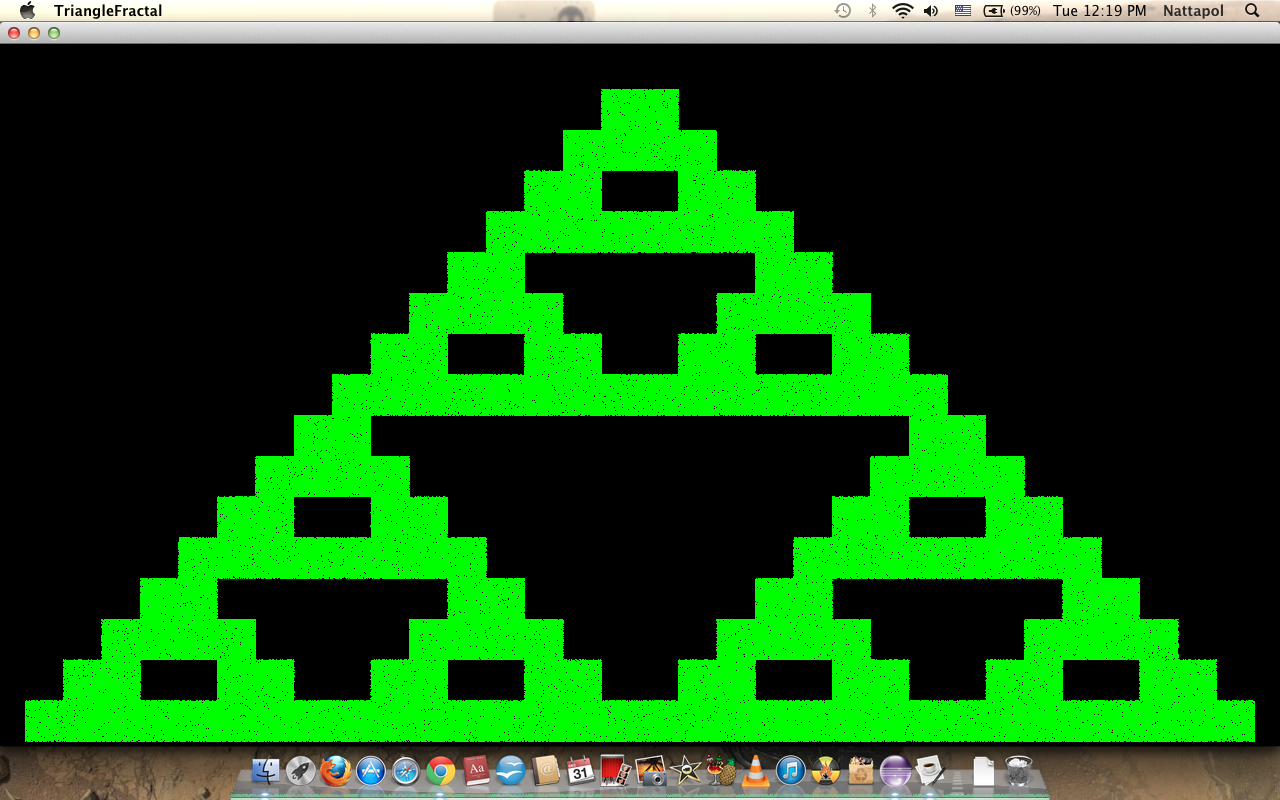
จำนวนครั้งของ recursive n=5



จำนวนครั้งของ recursive n=6



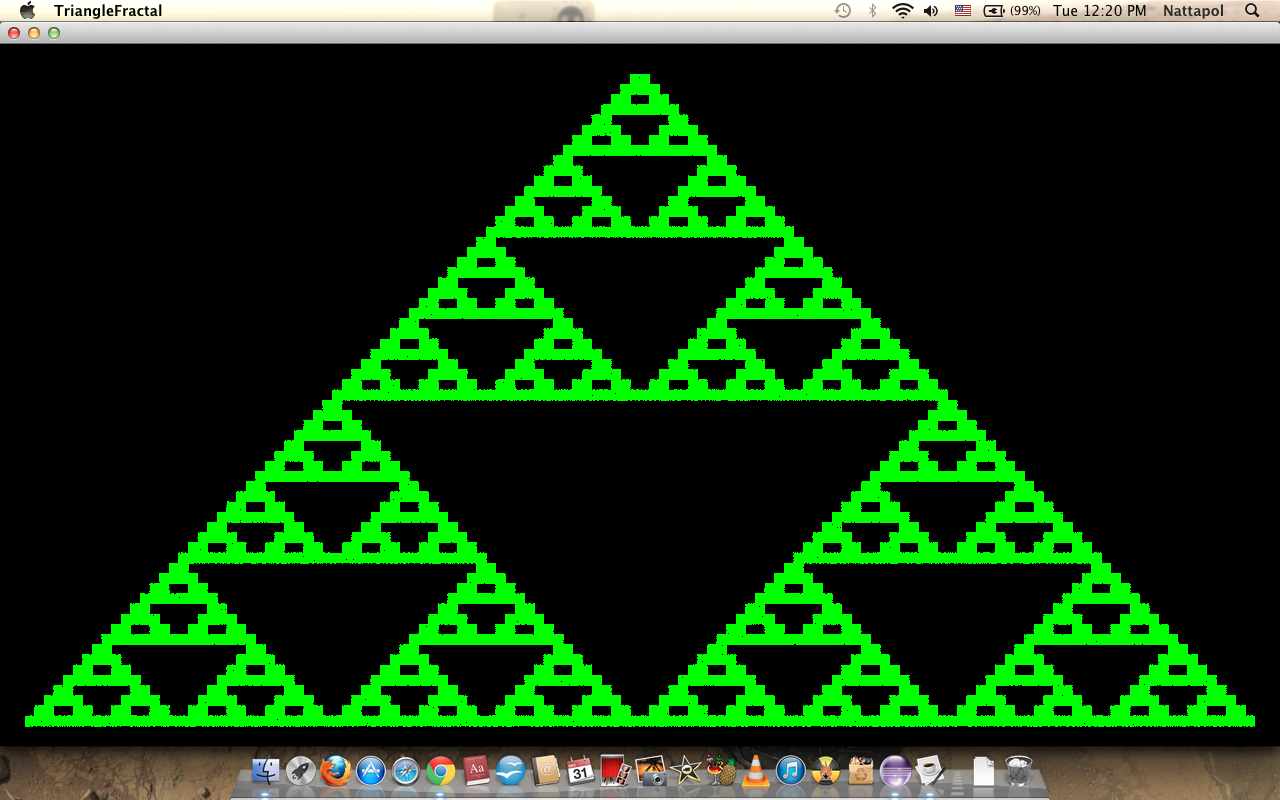
จำนวนครั้งของ recursive n=7



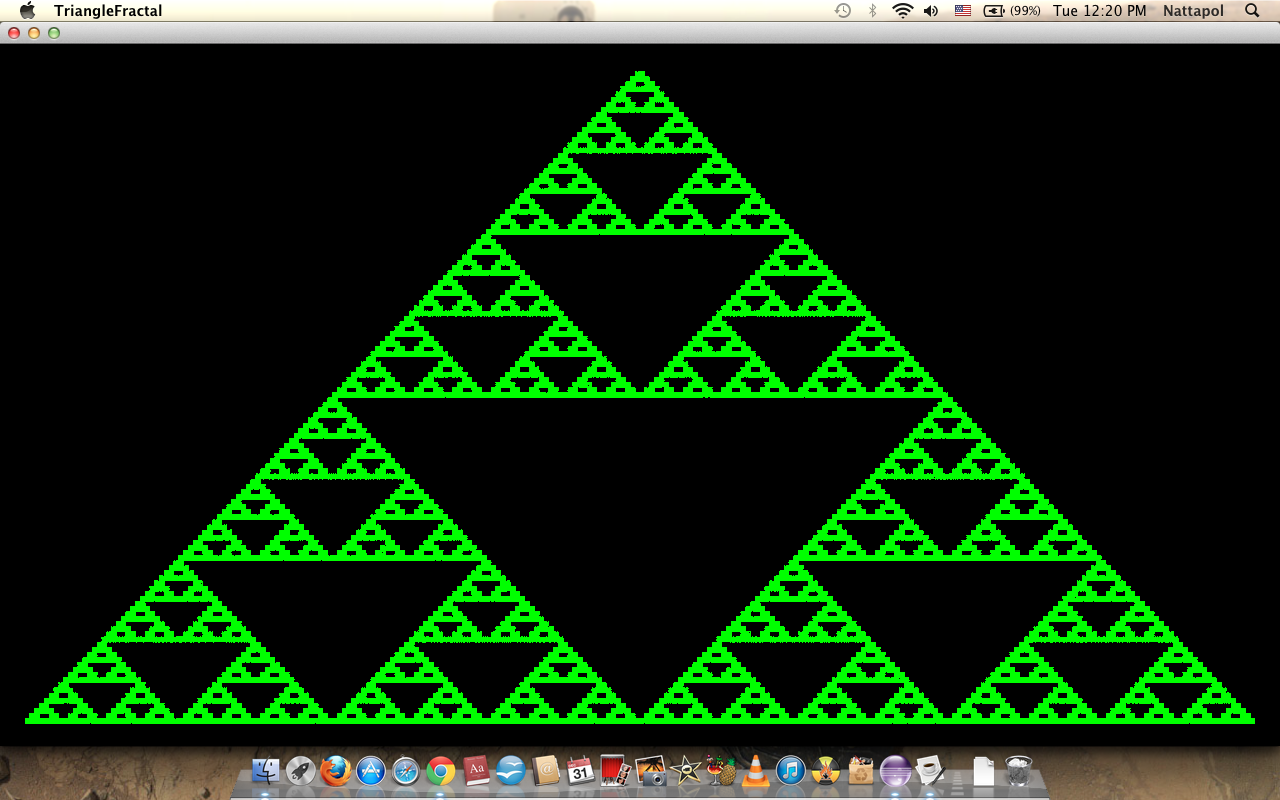
จำนวนครั้งของ recursive n=30





EPT








[ view entry ] ( 4458 views )   |  permalink  |  $star_image$star_image$star_image$star_image$star_image ( 2.9 / 454 )

<<First <Back | 1 | 2 | 3 | 4 | 5 | Next> Last>>